Python Sets - Common Data Structures

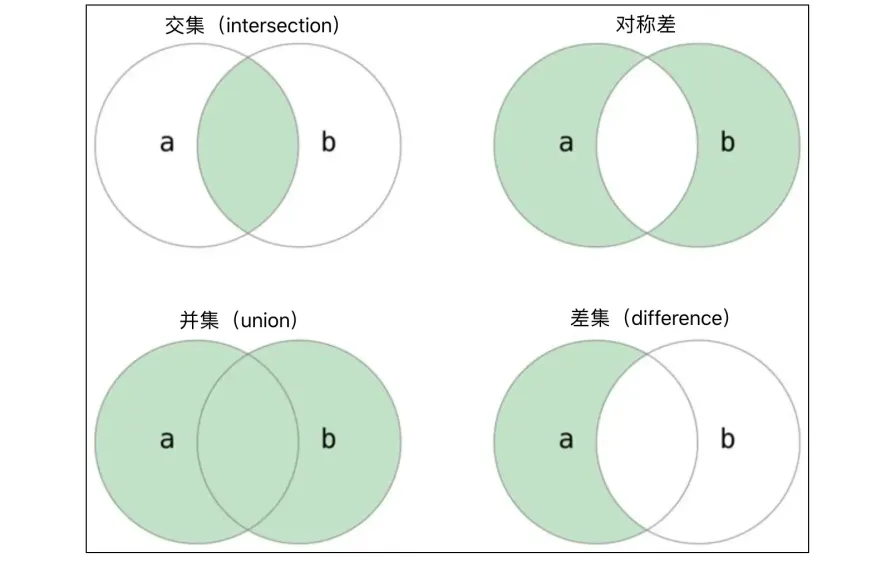
After learning about lists and tuples, let’s learn about another container data type called a set. Speaking of sets, everyone must be familiar with this concept from mathematics textbooks. If we treat a certain range of definite, distinguishable things as a whole, then this whole is a set, and the various things in the set are called elements of the set. Usually, sets need to satisfy the following requirements:

1. Unordered: In a set, each element has the same status, and elements are unordered.
2. Distinct: In a set, any two elements are different, meaning elements can only appear once in a set.
3. Definite: Given a set and any element, the element either belongs to this set or does not belong to this set, one of the two must be true, and no ambiguous situations are allowed.

Python sets are not essentially different from mathematical sets. What needs to be emphasized is the unordered and distinct properties mentioned above. The unordered property means that elements in a set do not have a certain order like elements in a list, and cannot be accessed through index operations. Sets do not support index operations. Additionally, the distinct property of sets determines that sets cannot have duplicate elements, which is also what distinguishes sets from lists. We cannot add duplicate elements to a set. Set types must support in and not in membership operations, so we can determine whether an element belongs to a set, which is the definiteness of sets mentioned above. Set membership operations perform better than list membership operations, which is determined by the underlying storage characteristics of sets. We won’t discuss this here for now, just remember this conclusion.

Note: Sets use hash storage (scatter storage) at the bottom level. Readers who don’t understand hash storage can first read the explanation of hash tables on the “Hello Algorithm” website. Thanks to the author’s open source spirit.

Creating Sets

In Python, you can create sets using the {} literal syntax. There must be at least one element in {}, because an empty {} is not an empty set but an empty dictionary. Dictionary types will be introduced in the next lesson. Of course, you can also use Python’s built-in function set to create a set. To be precise, set is not a function, but a constructor for creating set objects. This knowledge point will be introduced when we explain object-oriented programming later. We can use the set function to create an empty set, or use it to convert other sequences into sets. For example: set('hello') will get a set containing 4 characters (the duplicate character l will only appear once in the set). In addition to these two methods, you can also use generator syntax to create sets, just like we used generator syntax to create lists before.

set1 = {1, 2, 3, 3, 3, 2}
print(set1)

set2 = {'banana', 'pitaya', 'apple', 'apple', 'banana', 'grape'}
print(set2)

set3 = set('hello')
print(set3)

set4 = set([1, 2, 2, 3, 3, 3, 2, 1])
print(set4)

set5 = {num for num in range(1, 20) if num % 3 == 0 or num % 7 == 0}
print(set5)

It should be reminded that elements in a set must be hashable types. So-called hashable types refer to data types that can calculate hash codes. Usually immutable types are hashable types, such as integers (int), floating-point numbers (float), boolean values (bool), strings (str), tuples (tuple), etc. Mutable types are not hashable types because mutable types cannot calculate definite hash codes, so they cannot be placed in sets. For example: we cannot use lists as elements in a set; similarly, since sets themselves are also mutable types, sets cannot be used as elements in a set. We can create nested lists (where list elements are also lists), but we cannot create nested sets. This must be noted when using sets.

Tip: If you don’t understand the concepts of hash codes and hash storage mentioned above, you can put it aside for now, because it doesn’t affect your continued learning and use of the Python language. Of course, if you’re a computer science major, not understanding hash storage is hard to forgive, so you need to catch up quickly.

Element Traversal

We can use the len function to get how many elements are in a set, but we cannot traverse elements in a set through index operations because set elements have no specific order. Of course, to traverse set elements, we can still use a for-in loop, as shown in the following code.

set1 = {'Python', 'C++', 'Java', 'Kotlin', 'Swift'}
for elem in set1:
    print(elem)

Tip: Look at the running results of the code above and experience the unordered nature of sets through the order of word output.

Set Operations

Python provides very rich operations for set types, mainly including: membership operations, intersection operations, union operations, difference operations, comparison operations (equality, subset, superset), etc.

Membership Operations

You can use the membership operations in and not in to check if an element is in a set, as shown in the following code.

set1 = {11, 12, 13, 14, 15}
print(10 in set1)      # False
print(15 in set1)      # True
set2 = {'Python', 'Java', 'C++', 'Swift'}
print('Ruby' in set2)  # False
print('Java' in set2)  # True

Binary Operations

Binary operations on sets mainly refer to set intersection, union, difference, symmetric difference, etc. These operations can be implemented through operators or through methods of the set type, as shown in the following code.

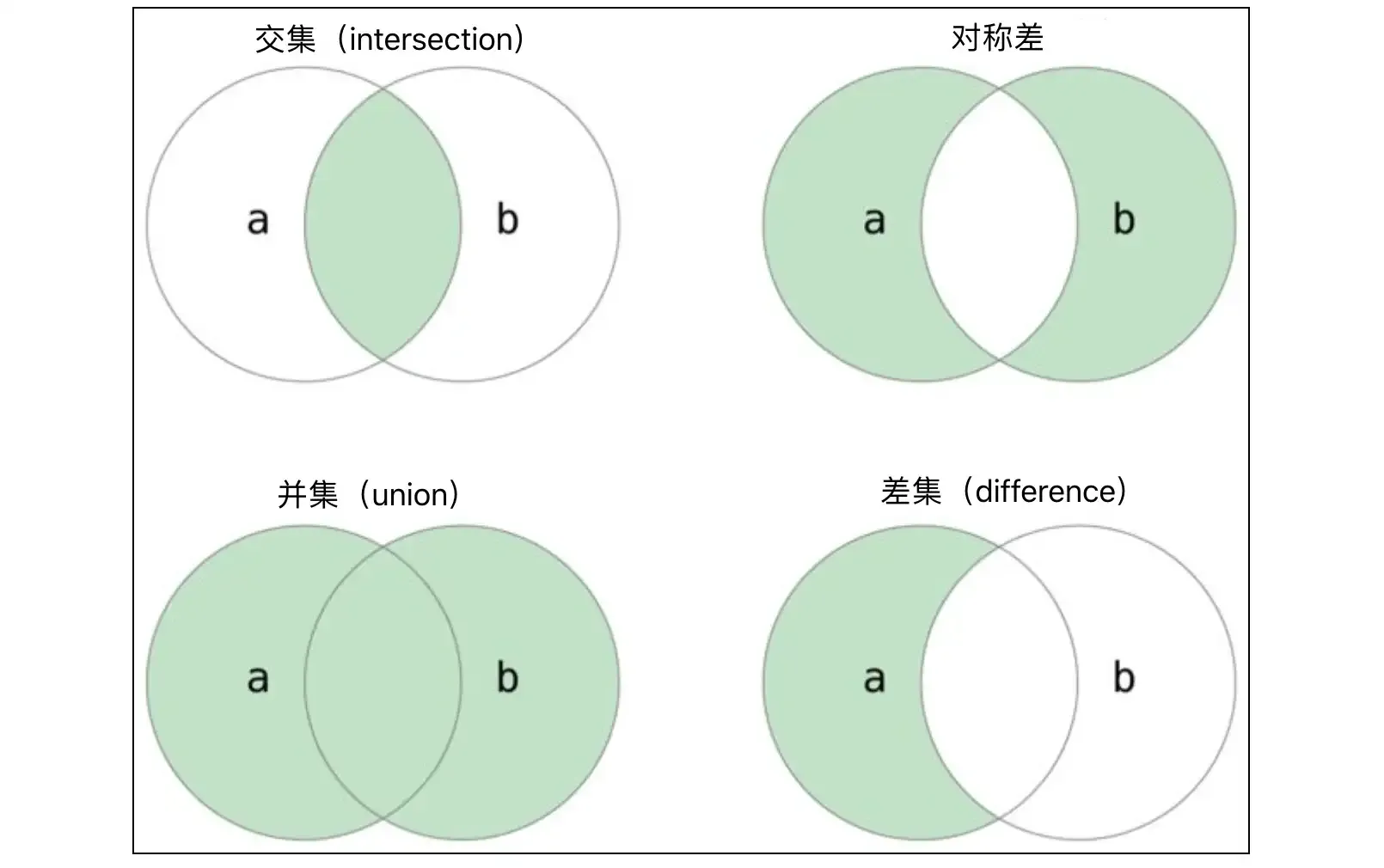
set1 = {1, 2, 3, 4, 5, 6, 7}
set2 = {2, 4, 6, 8, 10}

# Intersection
print(set1 & set2)                      # {2, 4, 6}
print(set1.intersection(set2))          # {2, 4, 6}

# Union
print(set1 | set2)                      # {1, 2, 3, 4, 5, 6, 7, 8, 10}
print(set1.union(set2))                 # {1, 2, 3, 4, 5, 6, 7, 8, 10}

# Difference
print(set1 - set2)                      # {1, 3, 5, 7}
print(set1.difference(set2))            # {1, 3, 5, 7}

# Symmetric difference
print(set1 ^ set2)                      # {1, 3, 5, 7, 8, 10}
print(set1.symmetric_difference(set2))  # {1, 3, 5, 7, 8, 10}

From the code above, you can see that for finding the intersection of two sets, the & operator and the intersection method have exactly the same effect, and using the operator is obviously more intuitive and the code is shorter. It should be noted that binary operations on sets can also be combined with assignment operations to form compound assignment operations. For example: set1 |= set2 is equivalent to set1 = set1 | set2, and the method that has the same effect as |= is update; set1 &= set2 is equivalent to set1 = set1 & set2, and the method that has the same effect as &= is intersection_update, as shown in the following code.

set1 = {1, 3, 5, 7}
set2 = {2, 4, 6}
set1 |= set2
# set1.update(set2)
print(set1)  # {1, 2, 3, 4, 5, 6, 7}
set3 = {3, 6, 9}
set1 &= set3
# set1.intersection_update(set3)
print(set1)  # {3, 6}
set2 -= set1
# set2.difference_update(set1)
print(set2)  # {2, 4}

Comparison Operations

Two sets can be compared for equality using == and !=. If the elements in two sets are exactly the same, the result of the == comparison is True, otherwise it’s False. If any element of set A is an element of set B, then set A is called a subset of set B, that is, for $\small{\forall{a} \in {A}}$, we have $\small{{a} \in {B}}$, then $\small{{A} \subseteq {B}}$, A is a subset of B, and conversely B can be called a superset of A. If A is a subset of B and A is not equal to B, then A is a proper subset of B. Python provides operators for determining subsets and supersets for set types, which are actually the very familiar <, <=, >, >= operators. Of course, we can also use the methods issubset and issuperset of the set type to determine the relationship between sets, as shown in the following code.

set1 = {1, 3, 5}
set2 = {1, 2, 3, 4, 5}
set3 = {5, 4, 3, 2, 1}

print(set1 < set2)   # True
print(set1 <= set2)  # True
print(set2 < set3)   # False
print(set2 <= set3)  # True
print(set2 > set1)   # True
print(set2 == set3)  # True

print(set1.issubset(set2))    # True
print(set2.issuperset(set1))  # True

Note: In the code above, set1 < set2 determines if set1 is a proper subset of set2, set1 <= set2 determines if set1 is a subset of set2, and set2 > set1 determines if set2 is a superset of set1. Of course, we can also use set1.issubset(set2) to determine if set1 is a subset of set2; and use set2.issuperset(set1) to determine if set2 is a superset of set1.

Set Methods

As we mentioned earlier, sets in Python are mutable types, and we can add elements to or remove elements from a set through set methods.

set1 = {1, 10, 100}

# Add element
set1.add(1000)
set1.add(10000)
print(set1)  # {1, 100, 1000, 10, 10000}

# Remove element
set1.discard(10)
if 100 in set1:
    set1.remove(100)
print(set1)  # {1, 1000, 10000}

# Clear elements
set1.clear()
print(set1)  # set()

Note: The remove method for deleting elements will raise a KeyError error when the element doesn’t exist, so in the code above we first use membership operations to determine if the element is in the set. The set type also has a pop method that can randomly delete an element from the set. This method returns (obtains) the deleted element while deleting it, whereas the remove and discard methods only delete elements and do not return (obtain) the deleted element.

The set type also has a method called isdisjoint that can determine if two sets have any common elements. If there are no common elements, this method returns True, otherwise it returns False, as shown in the following code.

set1 = {'Java', 'Python', 'C++', 'Kotlin'}
set2 = {'Kotlin', 'Swift', 'Java', 'Dart'}
set3 = {'HTML', 'CSS', 'JavaScript'}
print(set1.isdisjoint(set2))  # False
print(set1.isdisjoint(set3))  # True

Immutable Sets

Python also has an immutable type of set called frozenset. The difference between set and frozenset is like the difference between list and tuple. Since frozenset is an immutable type, it can calculate hash codes, so it can be used as an element in a set. Except for not being able to add and delete elements, frozenset is the same as set in other aspects. The following code briefly demonstrates the use of frozenset.

fset1 = frozenset({1, 3, 5, 7})
fset2 = frozenset(range(1, 6))
print(fset1)          # frozenset({1, 3, 5, 7})
print(fset2)          # frozenset({1, 2, 3, 4, 5})
print(fset1 & fset2)  # frozenset({1, 3, 5})
print(fset1 | fset2)  # frozenset({1, 2, 3, 4, 5, 7})
print(fset1 - fset2)  # frozenset({7})
print(fset1 < fset2)  # False

Summary

Set types in Python are unordered containers that do not allow duplicate operations. Because they use hash storage at the bottom level, elements in sets must be hashable types. The biggest difference between sets and lists is that elements in sets have no order, so elements cannot be accessed through index operations, but sets can perform binary operations such as intersection, union, and difference, and can also use relational operators to check whether there are superset, subset and other relationships between two sets.